The choice of degrees-of-freedom for a physical system is crucial for an efficient description. This was clearly expressed by Prof. Steven Weinberg in one of his fundamental rules for theoretical physicists:
You can use any degrees of freedom that you like to describe a physical system, but if you choose the wrong ones, you will be sorry.
The choice of degrees-of-freedom is linked with the concept of basic constituents of a physical system. It defines, in a sense, what possible interactions should be present in the chosen model and will also set some limits on the possible accuracy that can be achieved. In addition, our choice also determines the breakdown scale of our theory. Given these insights we can introduce effective theories, as a tool to understand physics in general. Effective theories take the view that questions about a physical property come also with a statement of the scale at which the property is measured, or viewed.
In our reserach we apply the formalism of effective field theories to various systems with different degrees of freedom:
- Atomic systems, such as helium clusters consisting of helium atoms.
- Halo nuclei, consisting of clusters of nucleons.
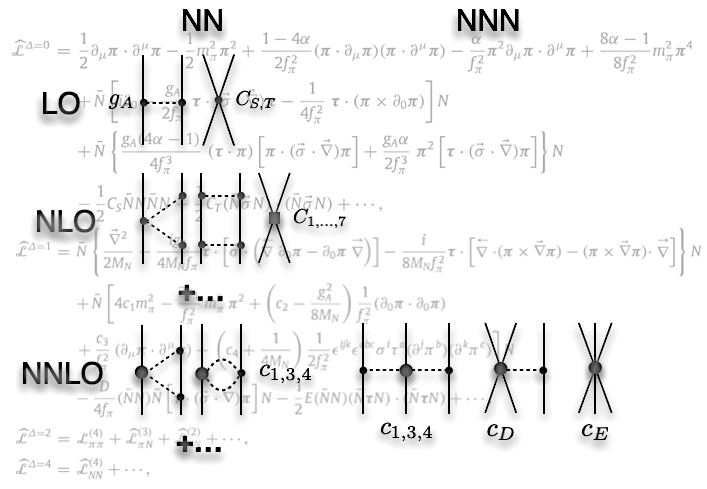
- Atomic nuclei, consisting of nucleons and pions.
- Dark matter-nucleus interactions, starting from dark matter particles and nucleons.
- Dark matter-electron interactions, with dark matter particles and electrons as degrees of freedom.