Past bachelor projects

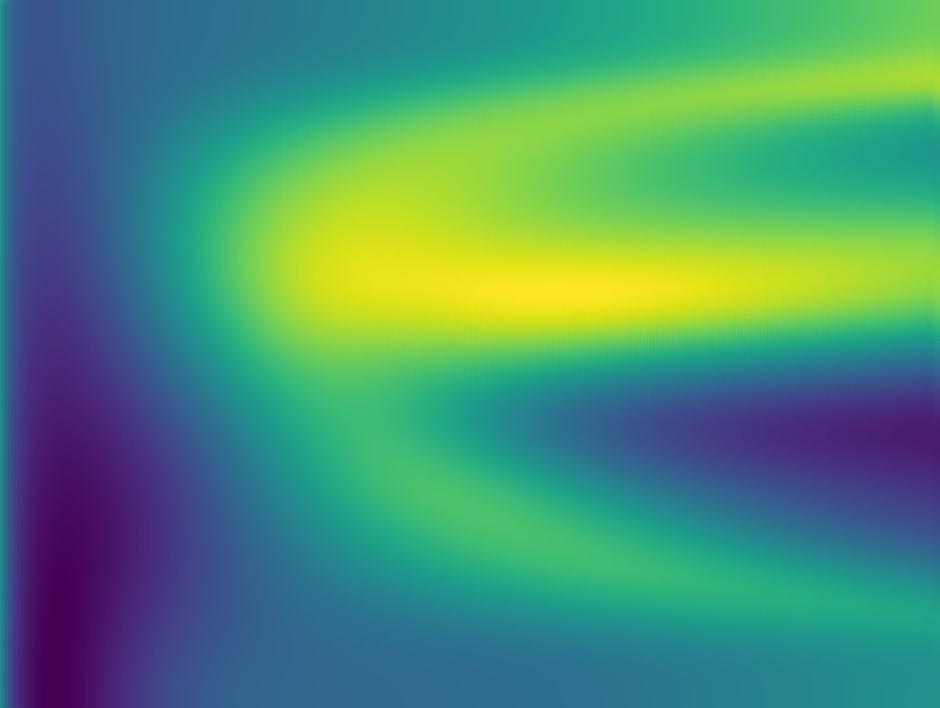
I följande rapport studeras det kvantmekaniska sammanflätningsfenomenet analytiskt och numeriskt. Specifikt undersöks i vilken utsträckning spridningsoperatorerna S och M sammanflätar en neutron och en proton med avseende på spinn i en spridningsprocess. M-matrisen beräknas numeriskt och även analytiskt utgående från en härledning av S. Den analytiska härledningen använder sig av lågenergiapproximationen att endast betrakta s-vågor.

Studien skiljer sig från tidigare forskning genom att behandla sammanflätning med utgångspunkt i M- operatorn istället för S-operatorn. Tidigare har också s-vågsapproximationen varit utgångspunkten i studier där sammanflätning i nukleon-nukleonspridning undersöks. En generalisering till en mer realistisk modell görs i detta arbete, vilket möjliggör analys vid högre energier samt av det spridningsvinkelbero- endet som uppstår.

De numeriska beräkningarna genomförs med en tillhandahållen kod och konvergensen för beräkningarna med avseende på partialvågor och samplingspunkter analyseras. Givet M-matrisen beräknas olika mått på sammanflätning med numeriska metoder, bland annat Monte Carlo-integration, som implementeras i Python. Två sammanflätningsmått presenteras och efter jämförelse används sammanflätningsstyrka för att studera fenomenet vid nukleon-nukleonspridning. Studien slår fast att det inte finns någon rörelseener- gi och spridningsvinkel i en nukleon-nukleonspridningsprocess som ger ett fullt sammanflätat uttillstånd i spinnrummet för alla möjliga initialtillstånd. På samma sätt finns det ingen kombination av rörelseenergi och spridningsvinkel som ger ett icke sammanflätat uttillstånd för alla möjliga initialtillstånd.

Sammanflätningsstyrkan för de analytiska S- och M-operatorerna undersöks. Skillnaden mellan deras sammanflätningsstyrka är att den för M konvergerar mot ett nollskilt värde i lågenergigränsen. Detta beteende observeras även i de numeriska resultaten. Sammanflätningsstyrkan för den analytiskt härledda M-matrisen jämförs med den numeriskt beräknade och överensstämmer relativt väl för energier upp till några få MeV. Från det analytiska uttrycket på M konstateras att om nukleonerna initialt har parallella spinn så uppstår ingen sammanflätning i interaktionen vid mycket låga energier. Detta verifieras även i jämförelsen med den numeriska undersökningen för specifika initialtillstånd.

Standardmodellen är den nuvarande teori som beskriver interaktionerna mellan elementarpartiklar. Trots att den har varit framgångsrik ger den inte en fullständig beskrivning av universum. Försöket att konstruera en mer fullständig teori har varit en av de huvudsakliga drivkrafterna inom högenergifysik. I denna rapport studeras fyra möjliga utökningar av fysiken i higgsområdet i standardmodellen, nämligen singlettskalärmodellen, sammansatt higgs-modellen, dubbel higgsdubblettmodellen och higgsportal mörk materia-modellen. I rapporten undersöks hur deras parametrar begränsas av experimentell data från CERN:s partikelaccelerator LHC. Undersök- ningen utförs genom maximum likelihood-skattning av parametrarna och Monte Carlo markovkedja-analys. De bayesianska a posteriorifördelningarna presenteras för parametervärdena och visar att standardmodellen fortfarande är kompatibel med resultaten, men att för vissa parametrar tillåter den nuvarande datan avvikelser från standardmodellens värden upp till 25%. Resultaten tillåter att upp till 8% av higgsbosonen kan sönderfalla till mörk materia vilket innebär att en eventuell kopplingsstyrka mellan mörk materia och higgsbosonen begränsas till 0,1. Singlettskalärpartikeln tillåts blandas med higgsbosonen upp till 18%. Sammansatt higgs-modellen kan falsifieras upp till energin 1,1 TeV. I dubbel higgsdubblettmodel- len kan inte en andra dubblett uteslutas, men ett scenario där den andra dubbletten inte kopplar till standardmodellen är möjligt. Sammantaget innebär resultaten att datan från LHC är kompatibel med standardmodellen.

Standardmodellen beskriver mycket av partikelfysiken väl, men det finns frågeställningar som kan undersökas hos kolliderare. Syftet med detta arbete är att undersöka möjligheterna hos föreslagna partikelkolliderare genom litteraturanalys och simuleringar, samt skriva en populärvetenskaplig artikel. De föreslagna kolliderarna som behandlas är Circular Electron Positron Collider (CEPC), Compact LInear Collider (CLIC), International Linear Collider (ILC), Super Proton Proton Collider (SPPC), Future Circular Collider både för leptoner och hadroner (FCC-ee respektive FCC-hh), samt Large Hadron Colliders uppgradering High Luminosity (HL-LHC). Litteraturanalysen sammanfattar några av de områden som kolliderarna kan undersöka, samt ger en översikt av några modeller bortom standardmodellen (BSM). Den första simuleringen behandlar framåt-bakåt-asymmetri för en Z-boson som skapar en toppkvark (t) och en antitoppkvark (¯t). Den andra simuleringen estimerar vilken luminositet som skulle behövas för att hitta nya partiklar i en hadronkolliderare vid en masscentrumsenergi på 100 TeV, som FCC-hh. Resultaten av litteraturanalysen och simuleringarna indikerar att nya kolliderare skulle kunna göra signifikanta upptäckter inom partikelfysik, vilka även kan bidra till ökad förståelse av universum. Dock behövs vidare utvärdering inför val av vilka kolliderare som bör konstrueras i framtiden. Utöver detta uppmanas vidare planering kring konstruktion och drift med ett miljöperspektiv i åtanke. Slutligen producerades en populärvetenskaplig artikel som förhoppningsvis kan bidra till allmänbildning.

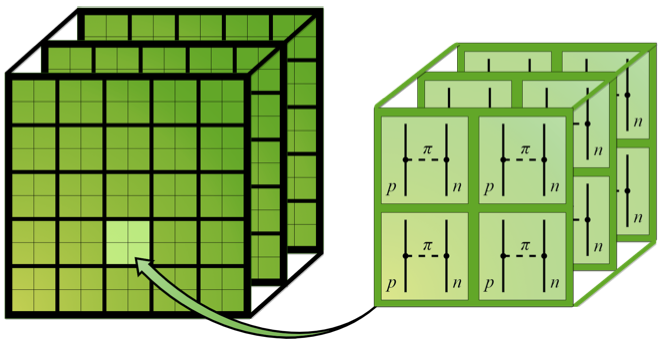
För att beskriva den starka kärnkraften med effektiv fältteori krävs noggrann kalibrering av kopplingskonstanterna i motsvarande potentialmodeller. Det ger upphov till ett flerdimensionellt inferensproblem som i sin tur kräver snabba numeriska beräkningar. Vi har därför undersökt möjligheten att genomföra effektiva beräkningar av spridningsfasskift genom att lösa Lippmann-Schwingerekvationen för elastisk proton-neutronspridning på en grafikprocessor (GPU). För att utnyttja parallelliseringsförmågan hos en GPU används gränssnittet CUDA i C++. Den numeriska lösningsmetoden, som baseras på upprepad lösning av en matrisekvation, har redan implementerats på en centralprocessor (CPU). Därför jämförs den totala exekveringstiden för CPU- och GPU-programmen, såväl som exekveringstiden per beräknat fasskift. Vi fann att GPU-programmet är snabbare än CPU-programmet vid beräkning av många fasskift samtidigt och att det därför finns goda möjligheter för mer effektiv kalibrering av kopplingskonstanterna med en GPU. Koden för att beräkna potentialmodellen är skriven för en CPU och har inte utvecklats i det här projektet. För att öka effektiviteten i våra GPU-beräkningar krävs dock effektivare hantering av potentialen. Vi drar slutsatsen att fortsatt optimering av vår GPU-kod samt anpassning för specifik hårdvara, som grafikkortet Nvidia Tesla V100, kan möjliggöra ännu snabbare beräkningar av elastisk proton-neutronspridning och därmed bidra till framsteg för att beskriva den starka kärnkraften.

Ej digitalt publicerat.

Modern cosmology proposes the existence of some unknown substance constituting 85% of the mass of the universe. This substance has been named dark matter and has been hypothesised to be composed of an as of yet unknown weakly interacting particle. Recently, the use of graphene as target material for the direct detection of dark matter has been suggested. This entails the study of the dark matter induced ejection of graphene valence electrons. In this thesis, we calculate the rate of graphene valence electron ejection under the assumption of different dark matter models, specifically where the squared modulus of the scattering amplitude scales like |q|2 or |q|4, where q is the momentum transfer. These models have not previously been considered. We initially derive analytic expressions for the electron ejection rate of these models, which we then evaluate numerically through the use of Python. The ejection rate is then plotted as a function of the electron ejection energy. We find that the electron ejection rate declines less rapidly in the models studied here than in the case of a constant scattering amplitude, i.e. the only case previously studied. The main challenge in these calculations is the high complexity of multidimensional integrals, the evaluation of which necessitated approximately 15,000 core hours.

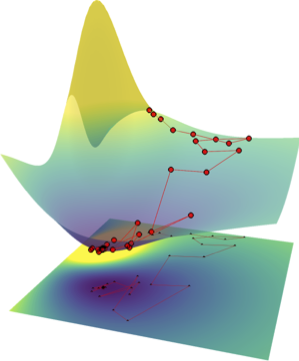
I denna studie applicerar vi Variational Quantum Eigensolver-algoritmen (VQE) på system i Lipkinmodellen för att bestämma grundtillståndsenergierna, med hjälp av en emulerad kvantdator utvecklad av Rigetti Computing. Variationsparametrarna optimeras med NelderMeadalgoritmen såväl som en Bayesiansk optimeringsalgoritm. Genom att utnyttja Hamiltoninanens kvasispinnsymmetri, reducerar vi Hamiltonianmatrisens dimension, varpå vi applicerar VQE-algoritmen på upp till 4 × 4-matriser, vilket svarar mot ett Lipkinsystem med sju partiklar. Utöver detta konstruerar vi nya ansatser och jämför dessa med den etablerade Unitary Coupled-Clusteransatsen. Vi genomför en omfattande analys av hur mätningarna på den emulerade kvantdatorn bör fördelas för att minimera felet. Med den optimala kombinationen av optimeringsalgoritm, ansats och antal samplingar per väntevärdesskattning, bestämmer vi grundtillståndsenergin, givet totalt 3 miljoner mätningar på den emulerade kvantdatorn, för olika värden på interaktionsparametern V /. Nelder-Meadalgoritmen och den Bayesianska optimeringsalgoritmen lyckas här beräkna grundtillståndsenergin för ett Lipkinsystem med sju partiklar inom 1.2 % respektive 0.7 % av den analytiska energin. Vidare observerar vi att den Bayesianska optimeringsalgoritmen presterar betydligt bättre för mindre totala antal mätningar på den emulerade kvantdatorn medan NelderMeadalgoritmen uppvisar ett mer stabilt beteende med fler mätningar. Baserat på detta tror vi att en kombination av de två algoritmerna kan vara att föredra framför var och en för sig.

I den här rapporten undersöker vi ett enkelt kvantmekaniskt system som simuleras på en emulerad kvantdator. Vi uttrycker ett enelektronsystem i en harmonisk oscillator-bas och söker efter dess grundtillståndsenergi. Metoderna för att hitta energin består av parametersvep samt algoritmen Variational Quantum Eigensolver (VQE) med COBYLA som optimeringsalgoritm. Simuleringarna körs på Rigettis emulerade kvantdator. Vi analyserar en ansats av typen Unitary Coupled Cluster (UCC) för systemets vågfunktion och jämför denna med en enklare ansats. Slutligen jämförs den uppskattade grundtillståndsenergin med en referenslösning. Utöver detta applicerar vi även en brusmodell för att undersöka resultatens känslighet för kvantmekaniskt brus. Vi finner att optimering är en bättre metod än parametersvep när Hamiltonianen utvecklas i ett större antal basvektorer, men optimeringsproblemet i sig blir för komplext för ett stort antal basvektorer. Vidare antyder våra simuleringar att känsligheten för brus ökar med antalet grindar hos en specifik vågfunktionsansats.

Webbplattformar är vanligt förekommande inom utbildning för att försöka förbättra studieresultat. De senaste årens effekter av digitalisering samt genombrott inom artificiell intelligens tyder emellertid på en outforskad potential i kombinationen av utbildning, webbteknik och artificiell intelligens. Som ett första försök att utforska den beskrivna potentialen, föreslår vi en flexibel och skalbar webbsida med en integrerad artificiell intelligens med förmågan att förutsäga universitetsstudenters studieresultat. Vi beskriver utvecklingen av webbsidan och artificiell intelligens samt ett experiment som undersö- ker interaktionen mellan student och artificiell intelligens. Vi argumenterar för att den utvecklade webbplatformen kan ligga till grund för ytterligare studier och föreslår flera inriktningar av framtida utveckling av utbildningsverktyget.

We compute the projected sensitivity to dark matter (DM) particles in the sub- GeV mass range of future direct detection experiments using germanium and silicon semicon- ductor targets. We perform this calculation within the dark photon model for DM-electron interactions using the likelihood ratio as a test statistic, Monte Carlo simulations, and back- ground models that we extract from recent experimental data. We present our results in terms of DM-electron scattering cross section values required to reject the background only hypoth- esis in favour of the background plus DM signal hypothesis with a statistical significance, Z, corresponding to 3 or 5 standard deviations. We also test the stability of our conclusions under changes in the astrophysical parameters governing the local space and velocity distribution of DM in the Milky Way. In the best-case scenario, when a high-voltage germanium detector with an exposure of 50 kg-year and a CCD silicon detector with an exposure of 1 kg-year and a dark current rate of 1 × 10^-7 counts/pixel/day have simultaneously reported a DM signal, we find that the smallest cross section value compatible with Z = 3 (Z = 5) is about 8 × 10⁻⁴² cm² (1 × 10⁻⁴¹ cm²) for contact interactions, and 4 × 10⁻⁴¹ cm² (7 × 10⁻⁴¹ cm²) for long-range interactions. Our sensitivity study extends and refine previous works in terms of background models, statistical methods, and treatment of the underlying astrophysical uncertainties.

Bayesiansk statistik i kombination med Markov chain Monte Carlo simulering- är ett mycket användbart verktyg inom dataanalysen. Mycket tack vare den förbättrade beräkningskapaciteten hos datorer samt effektiva algoritmer. Metoden används inom många naturvetenskapliga områden. Bayesiansk parameteruppskattning studerades genom att använda den generella Metropolis-Hastings algoritmen för Markov chain Monte Carlo simulering för en given modell. För att hitta sannolikhetsfördelningen för två okända modellparametrarna så itererade algoritmen i parameterrummet och tog stickprov. För ett tillräckligt stort antal iterationer så var stickproven fördelade som den sökta sannolikhetsfördelningen. Denna metoden kan vara fördelaktig då beräkningar inte behöver göras för alla punkter i parameterrummet. Metoden är snabb förutsatt att startpositionen för itereringen inte är allt för långt bort från det intressanta området. En jämförelse gjordes med metoden där sannolikheten beräknades för alla diskreta punkter i parameterrummet. Fördelen med denna metoden är att man får en helhetsbild av sannolikhetsfördelningen men för flerdimensionella modeller så blir denna metoden snabbt beräkningstung och ineffektiv.

Deciphering the nature of dark matter (DM) is one of the top priorities in modern physics. The DM direct detection technique will play a key role in this context in the coming years. The technique searches for signals of Milky Way DM particles interacting in low-background detectors located deep underground. So far, this technique has been used to search for DM particles heavier than atomic nuclei, assuming that DM primarily interacts with nucleons. Recently, the technique has been extended to the search for lighter DM particles with mass in the sub-GeV range and primarily interacting with electrons. This extension has opened a completely new window onto the search for galactic DM. Direct detection experiments searching for DM in the sub-GeV mass range exploit semiconductor detectors at cryogenic temperatures. The expected number of signal events in one of these experiments crucially depends on the velocity distribution of DM at detector. A standard assumption made in this context is that the velocity distribution at detector and in space coincide. However, as DM particles pass through our planet, they may scatter off particles in the Earth’s interior. Consequently, the Earth-scattering of DM is expected to perturb the velocity distribution of DM in space and generate a different distribution. It is the perturbed distribution that is actually probed at terrestrial detectors. This is what is referred to as the Earth shadowing effect. In this thesis, we present the first calculation of the Earth shadowing effect for sub-GeV DM, under the assumption that DM primarily interacts with electrons. We calculate the perturbed velocity distribution caused by Earth-scattering using a modified version of the publicly available EarthShadow code, here extended to properly model DM-electron interactions in the Earth. The perturbed velocity distribution is then used as an input in a modified version of the QEdark package to compute the expected number of signal events in a silicon detector. Focusing on a DM mass of 4MeV and considering three distinct parameterizations for the DM-electron cross section, we find that, when the Earth shadowing effect is included in the theoretical predictions, the expected number of signal events is decreased for certain detector locations on Earth. We conclude that the Earth shadowing effect indeed has an impact on underground detection experiments, and that our results must be taken into account in the interpretation of experimental results.

Gaussian processes (GPs) can be used for statistical regression, i.e. to predict new data given a set of observed data. In this context, we construct GPs to emulate the calculation of low energy proton-neutron scattering cross sections and the binding energy of the helium-4 nucleus. The GP regression uses so-called kernel functions to approximate the covariance between observed and unknown data points. The emulation is done in an attempt to reduce the large computational cost associated with exact numerical simulation of the observables. The underlying physical theory of the simulation is chEFT. This theory enables a perturbative description of low-energy nuclear forces and is governed by a set of low-energy constants to define the terms in the effective Lagrangian. We use the research code nsopt to simulate selected observables using chEFT. The GPs used in this thesis are implemented using the Python framework GPy. To measure the performance of a GP we define an error measure called model error by comparing exact simulations to emulated predictions. We also study the time and memory consumption of GPs. The choice of input training data affects the predictive accuracy of the resulting GP. Therefore, we examined different sampling methods with varying amounts of data. We found that GPs can serve as an effective and versatile approach for emulating the examined observables. After the initial high computational cost of training, making predictions with GPs is quick. When trained using the right methods, they can also achieve high accuracy. We concluded that the Matérn 5/2 and RBF kernels perform best for the observables studied. When sampling input points in high dimensions, latin hypercube sampling is shown to be a good method. In general, with a multidimensional input space, it is a good choice to use a kernel function with different sensitivities in different directions. When working with data that spans over many orders of magnitude, logarithmizing the data before training also improves the GP performance. GPs do not appear to be a suitable method for making extrapolations from a given training set, but performs well with interpolations.

Most of the matter in the Universe is unidentified and invisible, i.e. dark. Detecting dark matter particles from the Cosmos is arguably one of the most pressing research questions in science today. In the standard paradigm of modern cosmology, dark matter is assumed to consist of weakly interacting massive particles, which may annihilate in pairs into gamma photons. Such annihilations give rise to a measurable gamma ray flux, the amplitude of which is proportional to a so-called J-factor. Current J-factor calculations usually neglect dark matter self-interactions. However, dark matter self-interactions are compatible with current astrophysical observations, and can potentially solve long-standing problems regarding the formation and evolution of galaxies. The purpose of this thesis is to perform the first self-consistent J-factor calculation which includes dark matter self-interactions. This calculation is based upon the combined use of nonrelativistic quantum mechanics and Newtonian galactic dynamics. The formalism developed in this thesis has been applied to a sample of 20 dwarf spheroidal galaxies, which are known to be dark matter dominated astrophysical objects. For each galaxy in the sample, a likelihood analysis based on actual stellar velocity data has been performed in order to extract the distribution of dark matter in the galaxy, and estimate the induced error on the associated J-factor. We have found that the J-factors for self-interacting dark matter can be larger than standard J-factors by several orders of magnitude. Previous attempts to include dark matter self-interactions in the J-factor calculation neglect the details of the dark matter distribution in dwarf spheroidal galaxies. We have shown that this approximation leads to relative errors on the J-factors as large as two orders of magnitude. A paper illustrating these results is currently in preparation and is to be submitted to JCAP (impact factor 5.634).

The next decade of searches in the field of dark matter will focus on the detection of gamma rays from dark matter annihilation in dwarf spheroidal galaxies. This dark matter-induced gamma ray flux crucially depends on a quantity known as the Jfactor. In current research, the J-factor calculations does not include self-interaction between the dark matter particles, but there are indications on galactic scales that dark matter is self-interacting. The purpose of this thesis is to introduce a thorough generalisation of the J-factor to include a self-interacting effect and to compute the factor for 20 dwarf spheroidal galaxies orbiting the Milky Way. We thoroughly study the fundamental theory needed to compute the J-factor, based on Newtonian dynamics and non-relativistic quantum mechanics. A maximum likelihood formalism is applied to velocity data from dwarf spheroidal galaxies, assuming a Gaussian distribution for the line of sight velocity data. From this we extract galactic length and density scale parameters. The acquired parameters are then used to compute the J-factor. Using a binning approach, we present an error estimate in J. The used method is compared to previously published results, by neglecting self-interaction. We perform the first fully rigorous calculation for the J-factor, properly taking into account the dark matter velocity distribution. We can deduce that a previously used approximation of the self-interaction overestimates the J-factor by 1.5 orders of magnitude. Furthermore, we confirm that our method produces three to four orders of magnitudes larger values compared to J-factors without self-interaction.

Machine learning is a method to develop computational algorithms for making predictions based on a limited set of observations or data. By training on a well selected set of data points it is in principle possible to emulate the underlying processes and make reliable predictions. In this thesis we explore the possibility of replacing computationally expensive solutions of the Schrödinger equation for atomic nuclei with a so-called Gaussian process (GP) that we train on a selected set of exact solutions. A GP represents a continuous distribution of functions defined by a mean and a covariance function. These processes are often used in machine learning since they can be made to emulate a wide range of data by choosing a suitable covariance function. This thesis aims to present a pilot study on how to use GPs to emulate the calculation of nuclear observables at low energies. The governing theory of the strong interaction, quantum chro- modynamics, becomes non-perturbative at such energy-scales. Therefore an effective field theory, called chiral effective field theory (chEFT), is used to describe the nucleon-nucleon interactions. The training points are selected using different sampling methods and the exact solutions for these points are calculated using the research code nsopt. After training at these points, GPs are used to mimic the behavior of nsopt for a new set of points called prediction points. In this way, results are generated for various cross sections for two-nucleon scattering and bound-state observables for light nuclei. We find that it is possible to reach a small relative error (sub-percent) between the simulator, i.e. nsopt, and the emulator, i.e. the GP, using relatively few training points. Although there seems to be no obvious problem for taking this method further, e.g. emulating heavier nuclei, we discuss some areas that need more critical attention. For example some observ- ables were difficult to emulate with the current choice of covariance function. Therefore a more thorough study of different covariance functions is needed.

This thesis explores a possible addition of a scalar boson to the Standard Model. Apart from a quadratic coupling to the Higgs boson, it couples to the photon and the gluon. To fully be able to explore this new boson, it is necessary to get acquainted with some of the vast background theory in form of quantum field theory. This involves the most fundamental ideas of relativistic quantum mechanics, the Lagrangian formulation, cross section, decay rate, calculations of scatteringamplitude, Feynman diagrams, the Feynman rules and the Higgs mechanism. To analyse the particle, it was necessary to use computer aid in form of FeynRules, a package to Mathematica, for retrieve the Feynman rules for the particle, and MadGraph 5 for numerical calculations of decay rate and cross section. This was used to find limits to coupling constants with in the Lagrangian to concur with experimental findings.

The nuclear force is a residual interaction between bound states of quarks and gluons. The most fundamental description of the underlying strong interaction is given by quantum chromodynamics (QCD) that becomes nonperturbative at low energies. A description of low-energy nuclear physics from QCD is currently not feasible. Instead, one can employ the inherent separation of scales between low- and high-energy phenomena, and construct a chiral effective field theory (EFT). The chiral EFT contains unknown coupling coefficients, that absorb unresolved short-distance physics, and that can be constrained by a non-linear least-square fitting of theoretical observables to data from scattering experiments. In this thesis the uncertainties of the coupling coefficients are calculated from the Hessian of the goodness-of-fit measure chi2. The Hessian is computed by implementing automatic differentiation (AD) in an already existing computer model, with the help of the Rapsodia AD tool. Only neutron-proton interactions are investigated, and the chiral EFT is studied for leading-order (LO) and next-to-leadingorder (NLO). In addition, the correlations between the coupling coefficients are calculated, and the s The nuclear force is a residual interaction between bound states of quarks and gluons. The most fundamental description of the underlying strong interaction is given by quantum chromodynamics (QCD) that becomes nonperturbative at low energies. A description of low-energy nuclear physics from QCD is currently not feasible. Instead, one can employ the inherent separation of scales between low- and high-energy phenomena, and construct a chiral effective field theory (EFT). The chiral EFT contains unknown coupling coefficients, that absorb unresolved short-distance physics, and that can be constrained by a non-linear least-square fitting of theoretical observables to data from scattering experiments. In this thesis the uncertainties of the coupling coefficients are calculated from the Hessian of the goodness-of-fit measure chi2. The Hessian is computed by implementing automatic differentiation (AD) in an already existing computer model, with the help of the Rapsodia AD tool. Only neutron-proton interactions are investigated, and the chiral EFT is studied for leading-order (LO) and next-to-leadingorder (NLO). In addition, the correlations between the coupling coefficients are calculated, and the statistical uncertainties are propagated to the ground state energy of the deuteron. At LO, the relative uncertainties of the coupling coefficients are 0.01%, whereas most of the corresponding uncertainties at NLO are 1%. For the deuteron, the relative uncertainties in the binding energies are 0.2% and 0.5% for LO and NLO, respectively. Moreover, there seems to be no obvious obstacles that prevent the extension of this method to include the proton-proton interaction as well as higher chiral orders of the chiral EFT, e.g. NNLO. Finally, the propagation of uncertainties to heavier many-body systems is a possible further application.

A recent theoretical study of quantum few-body tunneling implemented a model using a Berggren basis expansion. This approach leads to eigenvalue problems, involving large, complex-symmetric Hamiltonian matrices. In addition, the eigenspectrum consists mainly of irrelevant scattering states. The physical resonance is usually hidden somewhere in the continuum of these scattering states, making diagonalization difficult.

introduced and the Berggren basis expansion explained. The results show that the ability of the Jacobi-Davidson algorithm to locate a specific interior eigenvalue greatly reduces the computational times compared to previous diagonalization methods. However, the additional computational cost of implementing the Jacobi correction turns out to be unnecessary in this application; thus, the Davidson algorithm is sufficient for finding the resonance state of these matrices.

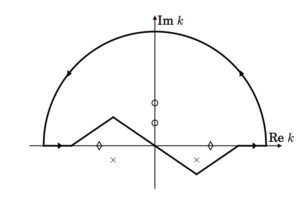
Resonances are important features of open quantum systems. We study, in particular, unbound and loosely bound nuclear systems. We model Helium-5 and Helium-6 in a few-body picture, consisting of an alpha-particle core with one and two valence neutrons respectively. Basis-expansion theory is briefly explained and then used to expand the nuclear system in the harmonic oscillator and momentum bases. We extend the momentum basis into the complex plane, obtaining the so-called Berggren basis. With the complex-momentum method we are able to reproduce the observed resonances in 5He. The 5He Berggren basis solutions are used as a single-particle basis to create many-body states in which we expand the 6He system. For the two-body interaction between the neutrons, we use two different phenomenological models: a Gaussian and a Surface Delta Interaction (SDI). The strength of each interaction is fitted to reproduce the 6He ground state energy. With the Gaussian interaction we do not obtain the 6He resonance, whereas with the SDI we do. The relevant parts of the second quantization formalism is summarized, and we provide details for its implementation.

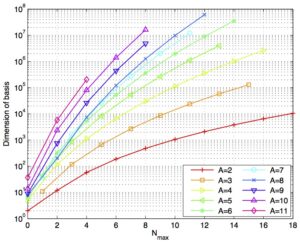
This thesis presents the results from a feasibility study of implementing calculations of transition densities for quantum many-body systems on FPGA hardware. Transition densities are of interest in the field of nuclear physics as a tool when calculating expectation values for different operators. Specifically, this report focuses on transition densities for bound states of neutrons. A computational approach is studied, in which FPGAs are used to identify valid connections for one-body operators. Other computational steps are performed on a CPU. Three different algorithms that find connections are presented. These are implemented on an FPGA and evaluated with respect to hardware cost and performance. The performance is also compared to that of an existing CPU-based code, Trdens.

rator in a fraction of the time used by Trdens, ran on a single CPUcore. However, the CPU-based conversion of the connections to the form in which Trdens presents them, was much more time-consuming. For FPGAs to be feasible, it is hence necessary to accelerate the CPU-based computations or include them into the FPGA-implementations. Therefore, we recommend further investigations regarding calculations of the final representation of transition densities on FPGAs, without the use of an off-FPGA computation.

This report aims to provide an insight into the particle physics of today, and into the research that goes on within the field. The focus is partly on the recent discovery of the Higgs boson, and partly on how software can be used to simulate processes in particle accelerators. Basic concepts of particle physics and the search for the Higgs boson are discussed, and experimental results, including those from the Large Hadron Collider, are compared with simulations made in MadGraph 5. Furthermore, simple new models of particle physics are created in FeynRules, in order to make simulations based on the models. To support the presentations of these aspects, some of the underlying theory is built from the ground up. Additionally, instructions are given on the usage of the programs FeynRules, for creation of models; MadGraph 5, for simulating processes in particle accelerators; and MadAnalysis 5, for data processing of the results obtained. The most significant results are simulations of processes commonly used for Higgs boson searches, with results in qualitative agreement with predictions and experimental data. The results also include consistent analytical and numerical calculations in a simple model with one particle.